上一期笔者写的《什么是机器学习》介绍说，机器学习是一种自动化构建模型的数据分析方法。计算机的算法利用输入的样本数据，迭代调整一个通用数学模型的参数，使得完成训练后，它能对应用对象的输入，返回一个合理的答案。测试人类智商的方法是被测试者参详样本，在选项中挑出最“合理”答案。机器学习模仿的正是这种类比判断的能力。

样本蕴含着数据的规律，在数学上是从问题的属性空间映射到答案空间的一个函数。机器学习的基本算法是从一族假设函数中，通过调整参数得到与之误差最小的函数。实践已经证明，这个学习机制非常成功地模仿了人类测试智商的功能，让机器从样本获得数据的模式，以此预测应用对象。

进一步深思，我们可能会疑惑，学习算法所得的是与样本误差最小的数学模型，为什么它能用来判断样本之外的对象？机器学习的算法以取得与样本最小误差为训练目标，如果仅仅是这样，让机器简单记忆这些样本就好了，而包含有这些样本的应用对象，它的数据模式往往多不胜数，有限的样本怎么能用来判别无限的可能？

上一期笔者写的《什么是机器学习》介绍说，机器学习是一种自动化构建模型的数据分析方法。计算机的算法利用输入的样本数据，迭代调整一个通用数学模型的参数，使得完成训练后，它能对应用对象的输入，返回一个合理的答案。测试人类智商的方法是被测试者参详样本，在选项中挑出最“合理”答案。机器学习模仿的正是这种类比判断的能力。

样本蕴含着数据的规律，在数学上是从问题的属性空间映射到答案空间的一个函数。机器学习的基本算法是从一族假设函数中，通过调整参数得到与之误差最小的函数。实践已经证明，这个学习机制非常成功地模仿了人类测试智商的功能，让机器从样本获得数据的模式，以此预测应用对象。

进一步深思，我们可能会疑惑，学习算法所得的是与样本误差最小的数学模型，为什么它能用来判断样本之外的对象？机器学习的算法以取得与样本最小误差为训练目标，如果仅仅是这样，让机器简单记忆这些样本就好了，而包含有这些样本的应用对象，它的数据模式往往多不胜数，有限的样本怎么能用来判别无限的可能？

解答这个问题，先要分析排除一些简单的情况。

如果应用对象的数据值只有有限的几个，当学习的样本包含了所有这些值，学习当然不成问题。这时采用通用数学模型来学习和死记硬背并无区别。只要判别输入是同于已知样本，预测等同于数据库的查询。逻辑推理是发现命题等价和蕴含关系的方法，如果能用逻辑推理，把问题输入归结为那些已知的样本，那就可以查询记忆来得出准确的答案。过去专家系统的人工智能就是在这个意义上如此工作。科学理论和应用的推理本质上也是如此。这依赖于非常强的假设。

在实践中，应用对象的数据值可能有无限或近乎无限多种。在这种情况下，传统的科学研究是通过分析简化，在理论上把它归结为简单的几种，应用时约减实际情况的细节，以纳入已知的条件，它可能工作很好，也可能因忽略关键的细节而出错。而专家系统的人工智能拘于形式逻辑，难以过滤细节，因此往往陷入困境。机器学习最适合应用于这种科学分析无能为力的情况。

再看一个简单的数值预测学习问题，来厘清学习问题的关键。对于单一输入求对应数值的预测问题，其数据的规律是个单输入函数，可以用待定参数w的多项式数学模型来学习。公式如下：

f(x)=w₀+w₁x+w₂x²+…+w_nxⁿ

数值预测的问题如果存在着模式：在一个区间里，当两个输入值相差很小时，对应的输出值相差也很小，则该函数可以用多项式来逼近。只要这个数学模型有足够的参数，在这个区间有足够多随机分布的样本，调整参数w总可以取得与样本很小的误差。那么它也能以很小的误差，在这个区间预测任何输入的对应输出值。不难想象，要取得学习成功必须满足以下几个条件。

1．应用对象的数据必须存在着某种规律或模式。

2．在应用的范围必须有足够多随机分布的样本数据，以覆盖各种情况。

3．机器学习的数学模型必须有足够灵活的表达能力，以能拟合应用对象的数据模式。

4．机器学习必须能控制数学模型的表达灵活性，以免过度拟合输入的样本。

这些条件同样适用于一般的机器学习。第一条指应用的对象，如果它们漫无规则，当然谈不上从中探知规律的学习和预测。第二条要求训练的样本必须包含足够多的数据规律信息，学习是从样本里汲取知识，它们必须充分蕴有。而深入探讨与学习能力相关的后两条意义更大。

上述例子应用对象的数据规律是一个单变量函数，样本表现为x-y平面上的一些点，学习算法调节数学模型的参数，让模型的函数曲线尽可能靠近这些点。如果模型只具有少量的参数，则它的函数曲线会比较“硬”。例如，只能表达直线或二次曲线，不能适应一些更复杂函数关系的样本点，表现为训练无法收敛，即数学模型不能拟合样本。另一方面，如果模型具有很多参数，表达非常灵活，则它的函数曲线会很“软”，调节参数很容易拟合这些样本点，也许应用对象的数据确是在一条直线上，结果模型的函数曲线蛇形穿过样本点，特别是在样本含有误差的情况下，虽然训练结果与样本点是完美吻合的，但在样本之外却有很大的误差，这叫过度拟合(overfitting)。学习算法里的通用数学模型，必须有足够的能力来拟合应用对象众多的样本，又能够防止过度拟合。这是学习功能的关键。我们从研究它的区分能力入手。

每个学习的机器可能有不同带参数的函数族作为通用的数学模型，同一个算法的机器，用不同的样本数据，赋予机器不同的知识和智能。机器的学习能力，只受数学模型对数据模式的表达能力所限，参数越多具有越强的表达能力。VC维度(VC dimension)用来量度这种数学模型的复杂性、灵活性或表达能力，更准确地说，是这函数族对数据模式的区分能力。这是20世纪60~90年代弗拉基米尔·万普尼克(Vladimir Vapnik)和阿列克谢·泽范兰杰斯(Alexey Chervonenkis)提出的统计学习理论中的核心概念。

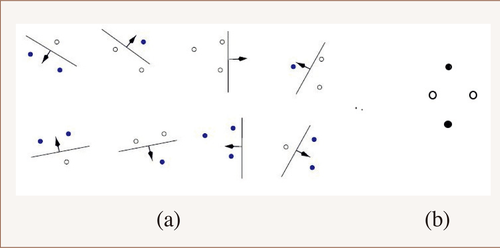
输出只有0和1的判断分类是最基本的情况，其他学习问题可以看作它的复合和变化。对于N个样本，把它们分为两类，一共有2^N种不同的模式。学习算法中带有参数的函数族H，能够对这N个样本进行二分的模式，最多的数量记为m_H(N)，它是一个随N增大的成长函数，以2^N为上界。如果m_H(N) = 2^N，则说N个样本能被H“粉碎(shatter)”，这时它能够实现这N个样本的任何一种二分模式，即对这里任何一种模式，都有H中合适参数的函数来实现这种模式的分类。VC维度D_H定义为能够被函数族H粉碎的最大样本数N。例如，只有一个参数w的域值分类函数 H={ f_w (x) | f_w (x)=x>w,   x,w∈R}，有m_H(N) =N+1，D_H=1；具有两个参数w₁，w₂在直线上的区间分类函数 H={ f_w1w2(x) | f_w1w2 (x)=(x>w₁)∧(x<w₂), x, w₁, w₂∈R}，有m_H(N) =N(N+1)/2+1，D_H=2；平面上一条直线，它能够区分3个点2³=8种分布模式（见图1(a)），但不能区分4个点16种分布模式中的两种（见图1(b)），所以2维线性分类函数的VC维度D_H=3。对于简单模型，VC维度大致上等于参数的数目。用数学归纳法可以证明，函数族H能够二分样本模式的最大数m_H(N)，在N到达VC维度之后，按N的多项式速度增长，这个多项式的最高幂次是D_H。

图1 (a)一条直线区分平面3个点的8种模式　(b)平面4个点的这种分布模式无法被一条直线区分

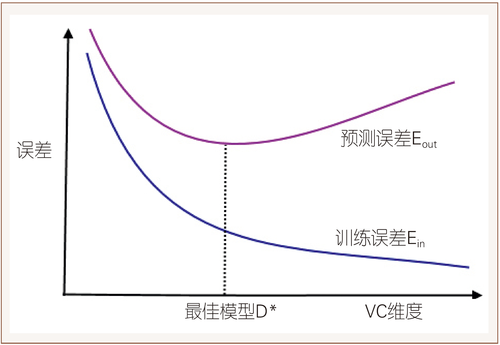
如果应用对象的数据存在着某种模式，这意味着，当随机供给的样本数增加到一定程度后，随后的样本终将会落入前面那些样本可能的模式之中，所以只要数学模型的VC维度足够大，便能实现这种分类模式。在这种情况下，无论增添多少样本，都会落入机器能够辨识的模式，表现为训练的误差会收敛。另一方面，VC维度太大，数学模型能够实现很多更为精细的模式，样本数据能被多种模式所拟合，训练可能选用了其中一种精细的模式，也许样本外的数据不能纳入这个适应面较窄的精细模式，所以VC维度太大，错失的可能性也会越大，这表现为模型过度拟合样本。尤其是在样本含有误差的情况，对样本之外的数据误差会更大（见图2）。

图2 数据模型复杂性与误差的关系

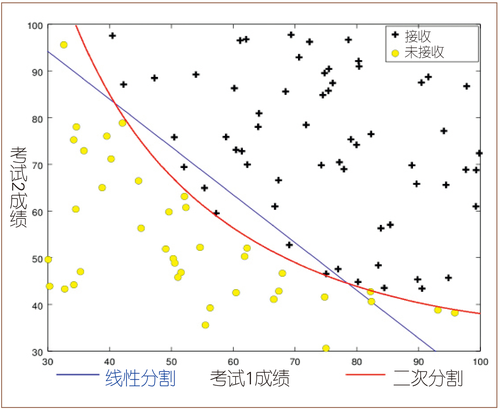
例如，两个输入的感知器(perceptron)或二维逻辑回归的数学模型 y = sign(w₁x₁ + w₂x₂ + w₀)，是平面上的一条直线，它的VC维度是3，能够实现辨识3个样本点所有可能的8种模式之一。对于线性可分模式的数据，再多的样本点也必定符合3个样本点所能划分的模式，只不过更多的样本点会更精确地调整参数，趋近应用对象数据分布的划分直线位置。如果样本含有误差，在较多的样本训练下也会得到纠正。如果采用VC维度更大的模型，如y = sign(w₁x₁ + w₂x₂ + w₀ + w₄ x₁²)，对于线性可分的数据，该模型经过训练也能够辨识所有的样本。但因为该数学模型是二次曲线，对样本外的判断误差较大，尤其是样本含有误差出现如图3那种分布模式，它们能被模型更精确地拟合，但表现出更大的样本外判断的误差。

图3 一次曲线和二次曲线分割样本点示意图

按VC维度概念所做的上述直观分析，用概率的语言更精确地表达是：以足够多随机选取的样本来训练，机器学习的预测误差率能以足够大的概率收敛于训练样本的误差率。估计这误差的概率上界，有如下Vapnik-Chervonenkis bound公式：

P ( |E_in(h) – E_out(h)| >ε| ∃h∈H ) ≤ 4m_H(2N) exp( -ε² N/8)

这里P是概率，ε是任给的一个小数值，H是数学模型的函数族，h是训练选出的函数，N是训练样本的个数，E_in(h)是h函数对训练样本预测的失误率，E_out(h)是对样本之外预测的失误率（数学期望），m_H(2N)是H能够二分2N样本的最多模式。只要函数族的VC维度是有限的，m_H(2N)对N按多项式速度增大远小于指数函数的减小。所以不等式的右边随N增大趋于0。这意味着只要训练的随机样本足够多，训练的误差足够小，那么对样本外的预测也能够取得很小的误差。对于这个误差上界的估计有许多研究，下面是其中之一，当ε很小时，误差概率上界有很大概率是：

E_out(h) ≤ E_in(h) + (8ln(2N) D_H/N - 8ln(ε/4)/N)^1/2

这式子说明，数学模型越简单，即参数变量少、VC维数D_H小，用非常多的样本训练后，它预测的准确性就越容易接近于在训练样本上检测到的精度。另一方面，我们知道数学模型越复杂，训练的结果对样本集的失误率E_in(h)就越小，它对样本的适应性就越好。成功的机器学习要求这两者都小，所以机器学习的算法调整模型参数，在追求尽量减小与样本误差的同时，也尽量减少起作用的模型参数，以便让模型成功辨识的同时，参与辨识数据模式起作用的VC维度尽可能小，这样对样本外的误差就会大大减少。这样的算法叫“正则化(regularization)”。

简单数学模型分类器的VC维数大致等于函数族中自由变量的数目。复合T个VC维度为D的分类器，可以取得T(D+1)(3ln(T(D+1))+2)的VC维度，这意味着多层神经网络可以用较少的参数实现较复杂的数据模式。所以，同样数目联接参数的深度网络要比浅层网络功能更强大。另一方面，对于一类应用对象，如图像处理，在深度网络中采用预设功能的处理层，如卷积层(CNN)有针对性地限制网络能辨识的模式，减少VC维度，可以取得更好的训练效果。所以深度学习要求很多设计技巧，有许多值得探索研究的地方。

数学模型VC维度的概念和概率统计的公式说明，只要应用对象的数据存在着模式规律，数学模型具有足够大的VC维度，便有可能通过样本的训练辨识这个模式。通过足够多的随机样本训练，它很可能精确地对应用对象进行预测。这便是机器学习的理论依据。它解释了机器学习在实践中取得成功的原因。

对于复杂的应用对象，机器学习需要巨量的参数和随机样本数据，它要求数据获取技术和支持这个巨量计算的计算机功能，这就是为什么一直到了大数据时代，人工智能才有了新突破。

数学的理论虽然证明了机器学习可以拥有很小的预测误差，但这只是在概率意义上的，而且要求使用足够多的随机无偏样本来训练才能达到。这不但意味着它的预测不像科学论断那样确定无疑，而且这概率意义下的准确率，也依赖于训练样本的随机无偏性，这种无偏性事实上是无法确定的。要取得训练成功往往也需要多种尝试。说到底，机器学习只是模拟了人的类比推测的功能，这是一种归纳式的推理，得不到科学理性的认可。我们虽然理解机器的学习机制，却无法用简单逻辑推演的跟踪来探知它所作判断的具体依据。学习的机器在无数参数错综复杂相互影响的乱麻中犹如直觉般做出的综合判断是难以剖析的。尽管它显示出令人惊异的智能，无可争辩地带来了科技革命，却把我们的理性监督排除在外。我们能够信赖这种如同占卜似的、带有误差的认知模式吗？下一篇《机器学习的认知模式》将讨论这问题。